Python numeric types

Introduction

Numbers are fundamental part of every programming language. Starting from Python 3.0 number types in Python programming language include three basic built-in types: integers, floats and complex numbers. Built-in means that Python already has those types included when you run and start type any program.

But there is more. Additional numeric types include Decimals and Fractions. In this case you have to include modules into your program in order to use them. This types are introduced if you want better precision control over floating types which we will discuss later in chapter.

At the end, there are several numeric subtypes like bitwise operators, Booleans, built-in functions and modules. In order to check what type some value belongs, you can use type () function or if you want to check if certain value is of specific type use isinstance () function.

Example

We can see that variable a is integer type:

>>> a = 3 >>> type(a) <class ‘int’>

Check if variable a is instance of int class:

>>> isinstance(3,int) True

Integer

Integers in Python are positive or negative whole numbers without decimal number. They size is unlimited because in Python 3, all integers types which were used before are now merged into one big integer type.

Examples

Define variable x and assign integer value 1:

>>> x = 1

Check the type of the variable:

>>> type(x) <class ‘int’>

Perform addition:

>>> x + 3 4

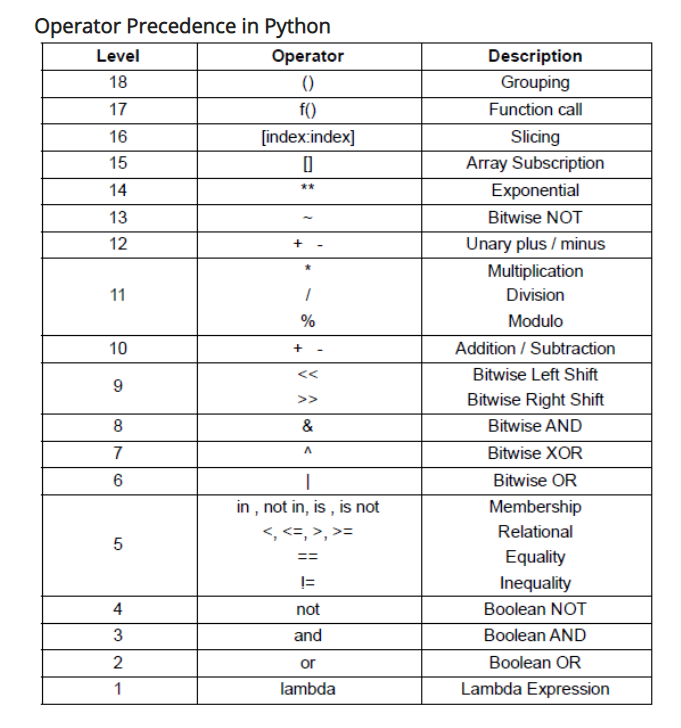
Precedence

Precedence inherits mathematical principles. Let take a look for an example:

>>> 1+2*3 7

First multiplication is performed (2*3) then result is added to number 1:

1 + 6 = 7. Multiplication has higher precedence and it is performed first.

But if we use parentheses result is different:

>>> (1+2) * 3 9

In this case, addition performed first and then result is multiplied with 3: 3 * 3 = 9. Parentheses have higher precedence over multiplication.

>>> x + 3 4

Higher level has higher precedence:

Operator overloading

It is important to mention the operator overloading feature in Python as well in any language and what actually means. We naturally use + operator for addition. Usually you take two numbers and perform addition. But + and other operators have different roles in Python. For example if you want to concatenate two strings you use +: print (“a”+”b”) = ab, or print (4 * “a”) = aaaa. They are multiple example which we will cover across Python sessions.

Conversions

Hexadecimal numbers

Hexadecimal numeric system that represents numbers with base 16. Numbers in hexadecimal system go from 0 to F.

DECIMAL	HEX
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10	A
11	B
12	C
13	D
14	E
15	F

In Python, hexadecimal numbers are presented with 0x symbol:

>>> 0xA 10

Hexadecimal number A which has value of 10 in decimal world.

0xAA = 10 * 16**1 + 10*16**0 = 160 + 10 = 170

Let’s put this into Python:

>>> (170,10 * (16 ** 1) + 10 * (16**0)) (170, 170)

Octal numbers

Octal numeric system that represents numbers with base 8. Numbers in hexadecimal system range from 0 to 7. Represented in Python by notation 0o.

DECIMAL	OCTAL
0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7

In Python octal numbers are presented with 0o symbol:

>>> 0o77 63

Let’s do the manual conversion:

0o77 = 7 * 8**1 + 7 * 8**0 = 56 +7 = 63

>>> (0o77, 7 * 8 ** 1 + 7 * 8 ** 0) (63, 63)

Binary numbers

Binary numeric system that represents numbers with base 2 and range from 0 to 1. Represented in Python by notation 0b. These numbers are recognized by computer and all numbers convert to 0 or 1 at the end.

>>> 0b111 7

Let’s do the manual conversion:

111 = 1 * 2 * * 2 + 1 * 2 **1 + 1 * 2 **0 = 4 + 2 + 1 = 7

>>> (7,0b111) (7, 7)

Number system conversions

You can use built-in functions to convert decimal numbers to hex, octal or binary:

>>> (hex(128),oct(128),bin(128)) (‘0x80’, ‘0o200’, ‘0b10000000’)

Floats

Float is approximate-number data representing real numbers, presented in computer hardware as base 2 (binary) fractions. To display floats, Python relies on standard IEEE 754 specification which has certain rules how to store floating point numbers:

Sign (1bit – positive or negative)

Exponent (11 bits – exponential portion)

Mantissa (base) (52 bits – mantissa)

Sign x Base^exponent

For example number 0.01 is stored as 1 * 10^-2

Displaying real numbers in binary fraction leads to round-off errors because some numbers can’t be displayed correctly in computer hardware. For example number 0.3333333…. can’t be displayed because it has unlimited number 3 after decimal point.

Starting from Python 2.7 and above, all real numbers are displayed in friendly way:

>>> 0.1

0.1

But deep under, 0.1 and 0.10000000000000001 and 0.1000000000000000055511151231257827021181583404541015625 are all approximated by binary fraction 3602879701896397 / 2 ** 55 which is not exactly the same as given numbers, which means that for mantissa part, it is always limited to 52 bits.

To make the rounding problems no so visible, normally floating point numbers are printed without their last digit, which is rounded. This is exactly to hide the problems you do not wish to see.

Number 0.30000000000000004 will be rounded to 0.3.

Display issue can be easily tested with this simple operation:

>>> 0.1 + 0.1 + 0.1 – 0.3

5.551115123125783e-17

If you want to check how 0.1 and 0.3 are stored enter following syntax:

>>> print(f”{0.1:.55f}”)

0.1000000000000000055511151231257827021181583404541015625

>>> print(f”{0.3:.55f}”)

0.2999999999999999888977697537484345957636833190917968750

This combination of addition and subtraction can’t give exactly the 0.

Example (Comparing two “same” numbers)

a = 10

b = a / 77

c = b * 77

a == c

False

You can see that a is not equal c, because of rounding problems with number 77,

Binary representation of real number 0.1

Python presents 0.1 in binary fraction: 0.0001100110011001101 you can notice that there is pattern which is always repeating. Let’s remind ourselves how we convert decimal fraction to binary:

0.1 * 2 = 0.2 integer part fetch 0

0.2 * 2 = 0.4 integer part fetch 0

0.4 * 2 = 0.8 integer part fetch 0

0.8 * 2 = 1.6 Integer part fetch 1

0.6 * 2 = 1.2 integer part fetch 1

0.2 * 2 = 0.4 integer part fetch 0

0.4 * 2 = 0.8 integer part fetch 0

0.8 * 2 = 1.6 Integer part fetch 1

0.6 * 2 = 1.2 integer part fetch 1

0.2 * 2 = 0.4 integer part fetch 0

…

Starting from bottom final number: 0110011000

We stop when multiplication of fraction and number 2 is 1, but it never gets there. Because there is always repeating part of 0011 we have to stop somewhere because we don’t have unlimited memory stock.

Some calculations avoid rounding

You can easily reproduce the problem if you make intentionally such a calculation

>>> 0.1 + 0.2

0.30000000000000004

You can see that for some calculations Python avoids rounding. But why we have this strange result: 0.30000000000000004

Remember the story about IEEE754 where floats are stored in following notation:

Sign (1bit – positive or negative)

Exponent (11 bits – exponential portion)

Mantissa (base) (52 bits – mantissa)

Sign x Base^exponent

If you convert 0.1 to binary representation (see article above- Binary representation of real number 0.1):

0.00011001100110011001100110011001100110011001100110011

Significate can’t be below value of 1 so we have to represent number 0.1 in following way:

mantissa base exponent

1.10011001100110011001100110011001100110011001100110011 * 2 (-4)

Base is number 2 and exponent is -4.

Final representation of number 0.1 includes sign, mantissa and exponent:

sign mantissa exponent

0 1.10011001100110011001100110011001100110011001100 01111111011

Number 0.2 is displayed in the same way:

sign mantissa exponent

0 1.10011001100110011001100110011001100110011001100 01111111011

Addition of 0.1 and 0.2 gives following result

0.1 + 0.2 = 0.010011001100110011001100110011001100110011001100110100 which is exactly 0.30000000000000004

Type conversions

Float are also dominant when doing operations between integer and float. For example addition of integer and float produces float as result:

>>> 0.1 + 1

1.1

>>> type (1.1)

<class ‘float’>

Decimal numbers

Decimal are numbers which are based on floating-point model, designed for people who do calculations like in school. Computers must provide arithmetic that people learn in school. Decimal numbers can be represented exactly with precision you want. Decimals and floats are incompatible when it comes to arithmetic. By default Decimal will digit number depending on entered values. If values have one decimal point result will be decimal point. Exception is division with infinite decimal numbers (irrational numbers) where default precision number is 28.

Decimal numbers are not embedded in Python, you have to call module decimal to activate decimal numbers. Decimal number take strings as arguments (‘0.1’). Without quotes it is just another float number. Usually you use it when making applications (finance) with exact decimal representation or to control the level of precision.

Example:

Import decimal module:

>>> import decimal from Decimal

Calculate floats:

>>> 0.1 + 0.1 + 0.1 – 0.3 5.551115123125783e-17

Calculate Decimals:

>>> Decimal(‘0.1’) + Decimal(‘0.1’) + Decimal(‘0.1’) – Decimal(‘0.3’) 0.0

You can always check what is behind last decimal digit:

>>> x = decimal.Decimal(“0.2″) >>> x >>> print(f”{x:.20f}”) >>> 0.20000000000000000000

There is big difference, floats which are binary based displayed results which is not 0 but Decimals displayed 0.0.

Number of decimal points depends on highest numbers of decimal points for arguments:

>>> Decimal(‘0.1’) + Decimal(‘0.1’) + Decimal(‘0.1’) – Decimal(‘0.30’) 0.00

Results is 0.00, number with two decimal points.

Precision

Precision is set by default to 28 digits when doing division operations with irrational numbers:

>>> import decimal >>> decimal.Decimal(1) / decimal.Decimal(7) Decimal(‘0.1428571428571428571428571429’)

Precision can be set (example for 4 digits):

>>> decimal.getcontext().prec = 4 >>> decimal.Decimal(1) / decimal.Decimal(7) Decimal(‘0.1429’)

When talking about money you can set precision to 2:

>>> decimal.getcontext().prec = 2 >>> pay = decimal.Decimal(str(1999 + 1.33)) >>> pay >>>Decimal(‘2000.33’)

Temporary reset precision:

>>> import decimal >>> with decimal.localcontext() as ctx: … ctx.prec = 2 … decimal.Decimal(‘1.00’) / decimal.Decimal(‘7.00’) Decimal(‘0.14’) >>> decimal.Decimal(‘1.00’) / decimal.Decimal(‘7.00’) Decimal(‘0.1428571428571428571428571429’)

Rounding

If we set decimal precision to 1, during division operations result will always be lower number by default:

>>> import decimal >>> x = decimal.Decimal(5) >>> y = decimal.Decimal(2) >>> z = x/y >>> z Decimal(‘2.5’) >>> decimal.getcontext().prec=1 >>> z = x/y >>> z Decimal(‘2’)

You can change the behaviour:

>>> decimal.getcontext().rounding=decimal.ROUND_HALF_UP >>> z = x / y >>> z Decimal(‘3’)

sqrt

The sqrt method allows us to get the square root of any Decimal with the designated level of precision:

>>> import decimal >>> decimal.getcontext().prec=10 >>> x=decimal.Decimal(2).sqrt() >>> x Decimal(‘1.414213562’)

 

Fractions

Fractions provides support for ration number arithmetic and representing fraction number in the same way the Decimal numbers. To use Fraction you need to import floating module just like you need to import decimal module to use Decimal numbers. Fraction instance can be constructed from strings, integers, floats, decimals and rational numbers. Fractions are immutable and hash able inheriting abstract base class numbers. Rational.

Let’s take a look a basic math operations with Fractions:

>>> from fractions import Fraction >>> x = Fraction(1,2) >>> y = Fraction(1,2) >>> x Fraction(1, 2) >>> y Fraction(1, 2) >>> x + y Fraction(1, 1) >>> Fraction(‘0.25’) + Fraction(‘1.25’) Fraction(3, 2) >>> x * y Fraction(1, 4) >>> x – y Fraction(0, 1) >>> x / y Fraction(1, 1)

Floats and fractions

Fractions can take floats as arguments but it that case, display will not be nice:

>>> Fraction(1.1) Fraction(2476979795053773, 2251799813685248)

If we put quotes that means that we are passing string as argument and result is completely different:

>>> Fraction(‘1.1’) Fraction(11, 10)

Other example of Fractions:

>>> Fraction(2.25) Fraction(9, 4) >>> Fraction(‘-.125’) Fraction(-1, 8) >>> Fraction(123) Fraction(123, 1) >>> 1 / 3 0.3333333333333333 >>> from fractions import Fraction >>> Fraction(1,3) Fraction(1, 3)

Fraction conversions

It is possible to convert between float and fraction types. To convert Float to fraction it is handy to use .as_integer_ratio () method which returns pair of integers with positive denominator:

>>> (2.5).as_integer_ratio() (5, 2)

Set value a to 1.5. Use the as_integer_ratio method to return pair of integer which are input values to Fraction method. Result is Fraction(3,2):

>>> a = 1.5 >>> b = Fraction(*a.as_integer_ratio()) >>> b Fraction(3, 2)

Another way:

>>> Fraction.from_float(1.25) Fraction(5, 4)

If you want to convert Fraction to float best way is to use float method:

Fraction(3, 2) >>> float(b) 1.5

When using mixed types in operations float is the winner:

>>> b Fraction(3, 2) Addition of Fraction and floats is float: >>> b + 2.0 3.5

Bitwise operators

Python like the C programming language includes operators which represents integers as strings of binary bits. It is handy when to use when dealing with serial ports, binary data, inspecting network packets and many more.

Number 1 is presented in binary form as: 0001

If you shift one bit to the left result will be 2 (0010):

>>> a = 1 >>> a << 1 2

Shifting number 2 one bit to the right gives back the number 1:

>>> a = 2 >>> a >> 1 1

Standard AND and OR operations looks like this:

a = 1 (0001)

a OR 2 = 0001 OR 0010 = 0011(3)

a AND 2 = 0001 AND 0010 = 0000(0)

>>> a = 1 >>> a | 2 3 >>> a & 2 0

Binary literals

How do you display integer in binary notation? You can do it like this:

>>> a = 0b0001 >>> a 1 a << 1 2

Let’s shift binary and display in binary literal:

>>> bin (a << 2) ‘0b100’

Hex literal looks like this:

>>> a = 0XAA >>> bin(a) ‘0b10101010’

Reverse process converting binary literal to integer:

>>> int(‘101101010’,2) 362

Python 3.1 and 2.7 introduced cool feature to display how many digits you need to display:

>>> a = 1000 (‘0b1111101000’, 10)

Booleans

Booleans is logic operator which has two values: True or False. But from Python point of view, Booleans are numbers. True and False are instances of class bool which is just one of the many subclasses of built-int type int. True and False have values 1 and 0 but different printing logic.

Following values are False in Python:

• None
• False
• any zero value
• empty sequence((),[],’’,{}
• __bool()__,__len()__ which returns 0 or false

If you type True + 1 the result is 2:

>>> True + 1 2

Checking the bool type with type gives:

>>> type(True) <class ‘bool’>

True is instance of int built-int type:

>>> isinstance(True,int) True

All integer values expect 0 are true:

>>> bool(2) True >>> bool(1) True >>> bool(0)

Evaluating the result is easy:

>>> 10 > 9 True >>> 10 < 9 False

>>> 10 > 9 True >>> 10 < 9 False

Standard AND, OR and not operators:

>>> True and True True >>> True and False False >>> True or True True >>> True or False True >>> not (True and True) False

Built-in functions and modules

Beside Python literals you can use standard built-in mathematical functions (abs, pow, min, max, sum) and module functions (rand, math) which include sin, cos, sqrt, floor, trunc, round and many more.

Examples:

>>> abs(-3) 3 >>> pow (2,2) 4 >>> 2 **2 4 >>> min (1,2,3) 1 >>> max (1,2,3) 3 >>> sum ((1,2,3)) 6

Some functions require math module.

Mathematical constants:

>>> import math >>> math.pi 3.141592653589793 >>> math.e 2.718281828459045

Floor function rounds number to next-lower integer

>>> math.floor(2.4) 2 >>> math.floor(2.6) 2 Trunc function drops decimal digit: >>> math.trunc(2.5) 2 >>> math.trunc(2.56) 2

Integer function converts decimal number to integer:

>>> int(3.239) 3

Square roots can be computed with built-in and module functions and expression.

Expression:

>>> 25 ** 0.5 5.0

Built-in function:

>>> pow(25,0.5) 5.0

Module function:

>>> math.sqrt(25) 5.0

One of the interesting module function is random function which randomly picks floating and integer numbers:

>>> import random >>> random.random() 0.5590639592013747 >>> random.randint(1,5) 5